^{Picture: Marshall, Alfred. Principles of Economics. Palgrave Classics in Economics. Basingstoke; New York: Palgrave Macmillan, 2013.}

Mathematical Economics in the 19th Century

A historical glimpse of how economists of the 19th century debated the usefulness of mathematics to economics

“As I see it, the economics profession went astray because economists, as a group, mistook beauty, clad in impressive-looking mathematics, for truth.” –  Paul Krugmann^[1]

 

The financial crisis of 2007/8 came as a tremendous shock to the economic profession, in which it was previously believed to have mastered how to tame the business cycle. Some of the criticism aimed at heavily mathematised neoclassical models bearing little resemblance to the real world. But although the excessive use of mathematics has become more frequently contested in the aftermath of the crisis, mathematics has lost little of its dominance over the field.^[2] Contemporary economics is still heavily formalised and mathematic models remain a standard tool of enquiry for nearly every economist. Although the mathematical method has become and remained an integral part of mainstream economics, its introduction was not a natural and smooth process. The introduction of mathematics into economics was not only a long process, but it also involved numerous attempts and failures to do so and was accompanied by a debate about its usefulness. Mathematics started to be introduced into economics in the 19th century and got increasingly accepted over the course of the 20th century. This can be seen in the substantial increase in the proportion of articles using algebra in economic journals. In 1930 ten per cent of the articles of the Economic Journal and American Economic Review used algebra, whereas in 1980 this proportion rose to 75 per cent.^[3] Or as Stigler et al. show, whereas in 1892 95% of the articles in the four leading journals of economics used neither a geometric representation nor mathematical notation, in 1990 only 5% of the articles used neither of those.^[4]

It is essential to every economic student to be acquainted with the introduction and the development of the methods and techniques used in the field to be able to critically assess them. In this essay, I aim to denaturalise the use of mathematics within economics, sketch its introduction into the field and acquaint the reader with the main debates around mathematical economics at that time to provide a historical dimension to the discussion about the mathematisation of economics. I, however, do not discuss the considered contribution to mathematical economics for its technical flaws and merits, as it would go beyond the scope and intent of this essay. Furthermore, as it would be an impossible task trying to draw any complete history of such a development, I focus mainly on the 19th century when mathematics was introduced. By doing so, I demonstrate that the adaption of mathematics into economics was not seen as a logical step of progress for the field but was controversially discussed instead. After sketching the debate around mathematical economics in the 19th century, William Stanley Jevons’s views and Alfred Marshall’s perspective are subsequently discussed to exemplify the debate in the 19th century, as contrasting their perspective seem very suitable to illustrate this debate. The last part then concludes.  

Mathematical Economics in the 19th century

The origin of mathematical economics is often dated back to the late 19th century and attributed to pioneers like Jevons, Walras and Fisher.^[5] The 1870s and the 1880s seem to have been a time of particularly intense discussion of whether mathematics is the right method for economics or not.^[6] Although these decades were crucially influential for the further development of the field, it’s important to note that the introduction of mathematics into economics started well before 1870 and was a long and drawn-out process.^[7] Even before the ground-breaking work of Antoine-Augustin Cournot in 1838, but especially afterwards, various attempts to include mathematics into economics were undertaken by different scholars.^[8] But as Theocharis notes, between Cournot’s work in 1838 and Jevon’s publication of “Theory of Political Economy” in 1871, the development of mathematical economics was still rather slow.^[9] In contrast to these mathematical attempts, the contributions of the classical economists are, except for a few uses of arithmetic, entirely discursive.^[10]

In the 19th century, numerous economists were interested in applying mathematical methods, but the mathematics of the time did often not provide sophisticated enough tools to address economic problems.^[11] And as an economist’s training didn’t involve the need to master mathematics, it doesn’t come as a surprise that many of the early economists using mathematics were engineers – as Charles Ellet, Jules Dupuit and Dionysus Larder – or had a background in other natural sciences.^[12] Because mathematics was not naturally applied to economics most authors felt the need to justify the use of mathematics as a tool of inquiry. Such justifications are seldomly seen in today’s economics and show that in the 19th century the use of mathematics was not per se accepted as a legitimate tool.

In his article in the ’Annales des Ponts et Chaussées’ in 1844, where the trained engineer Jules Dupuit discusses the utility of public works, he justifies the use of mathematics on the grounds that the variables in economics are quantitative – a line of argumentation later echoed by Jevons. Dupuit writes:

“So soon as it is realized,…, that political economy is concerned with quantities susceptible of a more or less, it must also be recognized that it is in the realm of mathematics.”^[13]

It becomes furthermore clear that he saw mathematics as a working and thinking tool as he closes his article: 

“They [the symbols and drawings of mathematics] are machines which, at a certain stage, can think for us, and there is as much advantage in using them as there is in using those which, in industry labour for US.”^[14]

This resonates with the work of Mary Morgan on the development of models within economics – of which many are mathematical or graphical – and demonstrates that early mathematical economists saw them often as a useful thinking tool, that helped them to stay consistent in their reasoning and work with rigor.^[15]

In his work in 1854, the Prussian economist Hermann Heinrich Gossen justified his mathematical framework more with the complexity of the economic realm:

“For the justification of this framework, it suffices to observe that economics concerns itself with the interplay of a variety of forces and that it is impossible to determine the resultant effect without calculus. For this reason, it is impossible to present the true system of economics without the aid of mathematics - a fact that has long been recognised in the case of pure astronomy, pure physics, mechanics and so forth.”^[16]

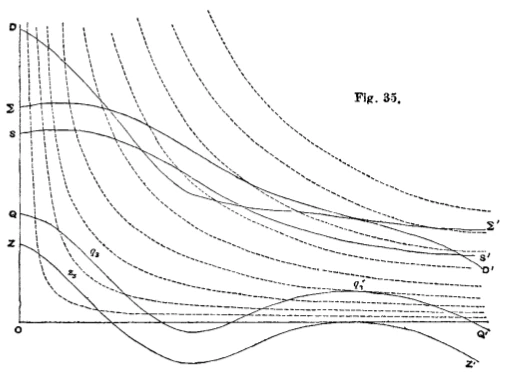
Gossen not only saw mathematics as a tool to manage the complexity of the economic realm but furthermore as a necessary precondition for pure economics. This quote reveals, furthermore, an active attempt to create a connection to the natural sciences, which was widely common among mathematical economist. This physics envy, as this phenomenon is often referred to, manifested itself in trying to make economics a rigorous science and was an important factor in promoting the use of mathematics.^[17] Creating an affinity between economics and natural sciences provided a justification to borrow concepts from natural sciences and make use of mathematical reasoning to discover general laws of economics. Portraying economics as a natural science was, furthermore, an attempt to endow economics with more authority. Almost all mathematical economists of the 19th century referred at some point to the natural sciences and their concepts when discussing economic questions. These attempts to incorporate physical concepts and analogies are very illustratively seen in the work of Irving Fisher, an original trained mathematical physicist, as he makes use of many drawings of such concepts. The famous American economist used many analogies and the language from physics to investigate economic phenomena.^[18] Below there are two illustrations out of Fisher’s ’The Purchasing Power of Money’, where he makes use of a mechanical and hydraulic model to address economic questions. As these examples are only thought as illustrations of the physics envy, they are not discussed any further.^[19]

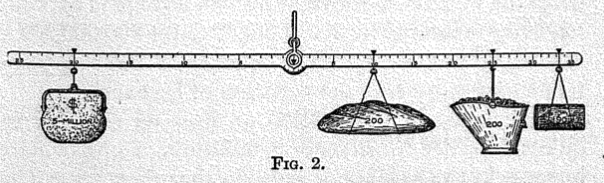
Figure 1: Fisher's mechanical balance of exchange to clarify the quantity theory of money.  ^[20]

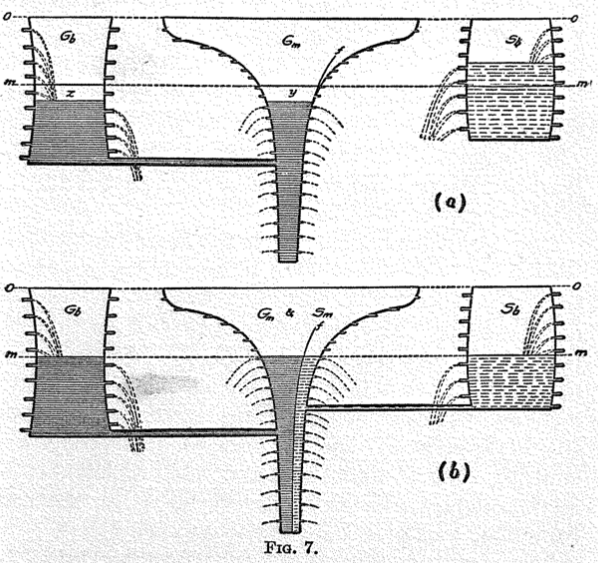
Figure 2: Fisher making use of hydraulics to model the purchasing power of money under a system of bimetallism [21]

But whereas 19th-century mathematical economists were looking at physics with a combination of envy and admiration, 19th-century physicists were hardly impressed when studying the concepts from the mathematical economists borrowed from their field.  Philip Mirowski illustrates in his book through various exchanges of letters between famous contemporary economists and respected physicists that these economists had very little to offer as an answer to the critical questions by these physicists interested in economics.^[22] Mirowski’s explanation for the failed communication on Pareto’s mathematical concepts between Hermann Laurent and Vilfredo Pareto is pretty straightforward:  “Laurent understood the physics, and Pareto did not.”^[23] Regardless of these critical comments by physicists, the physics envy was central to the development of the economic discipline. Mirowski emphasises the importance of physics for the development of economics, by stating that “physics was the dog and economics the tail throughout the whole of history of economic thought.”^[24]

But alongside the enthusiastic embrace of mathematics by its apologists like the ones above, there was a strain of economists, who were extremely skeptical of mathematical economics. Some opponents of mathematics like for example Jean-Baptiste Say didn’t see any use for mathematics in economics, on the ground that economics belongs to the domain of morals.^[25] Other economists opposing the use of mathematics argued that since the variables relevant for economics are based on human volition they are arbitrarily variable and therefore it was impossible to rigorously work with them.^[26] And some economists opposed the use of mathematics, because they didn’t think mathematics would add anything new to the field but only reformulate what was already known.^[27] As an example, one of the critics of excessive mathematical economics, John Elliott Cairnes, did concede that mathematics can be applied to economics, but strongly argued that mathematics cannot be the means to discover economic truths. He writes in the Preface to his second edition of ’The Character and Logical Method of Political Economy’ commenting Jevons’s work:

“So far as I can see, economic thrust are not discoverable through the instrumentality of Mathematics. If this view be unsound, there is at hand an easy means of refutation - the production of an economic truth, not before known, which has been thus arrived at; but I am not aware that up to the present any such evidence has been furnished of the efficacy of the mathematical method.”^[28]

As there were many different views on the use of mathematics, it is not evident how accepted mathematics was as a tool to do economics by the end of the 19th century. Historians agree on the fact that there were controversial discussions on the usefulness of mathematics during the 19th century. But although Margaret Schabas argues that “the mathematization of economic theory was already well under way in late Victorian England,” Weintraub notes that by the end of this century the question of mathematical economics was still an open one.^[29] The statistics above on the academic use of maths in economic journals tend to support Weintraub’s claim. And at least in 1885 chief editor Gustave de Molinari of the influential periodical ’Journal des Economistes’ felt the need to complement a publication of Walras paying homage to Gossen with a statement that doesn’t suggest that mathematics was well established within the economic profession:

“While publishing this article by one of our old and learned collaborators, we must in the first instance reserve our position on the usefulness, according to us too exaggerated, which he attributes to the application of the mathematical method to a science of observation such as ours.”^[30]

Therefore, it seems fairly evident that although there were many contributions to mathematical economics by the end of the 19th century the profession as a whole hasn’t yet completely accepted its introduction.

In the background of the discussion on the use of mathematics was also a methodological debate of deductivism vs. inductivism. A debate that was also prominent among the classics but, which is important to note, cannot be translated directly to the debate around mathematical economics.^[31] The battlegrounds, however, were often along similar lines. While for example, David Ricardo was a strong advocate of the deductive method among the classical economists, Malthus was more sceptical of the deductive method and more of an empiricist.^[32] In 1819 he wrote:

“The principal cause of error, and of the differences which prevail at present among the scientific writers on political economy, appears to me to be a precipitate attempt to simplify and generalize.”^[33]

Although Jevons seems to seek to portray Malthus as a proponent of the mathematical method, Malthus himself is pretty clear on the opening page of his ’Principles of Political Economy’ where he writes:

“…we shall be compelled to acknowledge, that the science of political economy bears a nearer resemblance to the science of morals and politics than to that of mathematics.”^[34]

This key methodological debate stretched over two centuries and accordingly in 1933 Keynes commented on the state of economics by taking side with Malthus:

“If only Malthus, instead of Ricardo, had been the parent stem from which nineteenth-century economics proceeded, what a much wiser and richer place the world would be today!”[35]

It was also mostly the criticism of the deductive method that made scholars from the German Historical School opponents of abstract mathematics in economics. And although most of the proponents of mathematical economics in the 19th century were also strong advocates of the deductive method, there were some mathematical economists perusing a more nuanced approach, as for example William Whewell, a pioneer of British mathematical economics. His methodological approaches stress the necessity to use the inductivist methods to formulate axioms and basic assumption but then use mathematics to work out the implications of these axioms and assumptions and draw conclusions.[36] This steering of a middle way between deduction and empiricism is later found in Marshalls approaches, as will be discussed later, and can be illustrated in Marshall’s endorsement of Gustav Schmoller’s statement in his ’Principles ’: “Induction and deduction are both needed for scientific thought as the left foot and the right foot are both needed for walking.”[37]

An important aspect of the development of mathematical economics was the changing focus of economics in the later 19th century. As Hudson and Hodgson argue, the introduction of marginalism in the 19th century narrowed the subject of economics to problems at the margins, which allowed mathematics to be applied.[38] For example, questions around the formation of wealth and its distribution among classes, which was of tremendous importance for classical economists, became less and less prominent, but the individual utility maximiser started to rise to fame – a concept that makes it much easier to mathematically reason with it. The important point to Hudson in that sense is „that no structural problems are recognized, no problems that cannot be solved by marginal quantitative adjustments in incomes, prices and wage levels, the money supply and the interest rate.”[39] As will be discussed in the case of Jevons, the reduction of the economic subject was deliberate step to enable the wide use of mathematics and lay the ground for its conquest of the profession. Furthermore, the narrowing of the field also came through the focus of many early mathematical economists on problems relating to engineering questions, as for example the discussion of transportation costs by Thünen and Launhard, which allowed mathematics to be used.[40] This shift in focus also gave economics a more mechanical outlook, that relates to the physics envy and contributed to the reification of economics and the human subject.[41] The reification of the human subject to a mechanical machine can be clearly detected in the works of Jevons and Edgeworth, and will be discussed in the next section.

As illustrated in this section, there was a lively discussion in the 19th century on the usefulness of mathematics for the economic profession with fierce advocates on each side. Of course, only a small glimpse of what was debated in the 19th century could be provided. The intent is to acquaint the reader with the main strains of the debates around mathematical economics at the time.[42] Equipped with the contextual background, the next part dives into the argumentation of Jevons, who was a strong proponent of the use of mathematics. Thereafter, Jevons’s argumentation is contrasted with the views of Alfred Marshall, who attempted to steer a middle ground.

William Stanley Jevons – the reification of economics

The English economist William Stanley Jevons (18835-1882) was one of the strongest and most successful proponents of mathematical economics. His ‘Theory of Political Economy’, published in 1871, was not only extraordinarily influential, it made also a strong case for the use of mathematical methods.[43] Jevons was not only convinced that mathematics was useful for economics, he even went so far as to state – echoing the argumentation of Jules Dupuit – that economics “must be mathematical, simply because it deals with quantities.”[44] His substantial contribution to economics stems not only from the conceptualisation of marginalism, but much more from his systematic arguments that economics called for the use of mathematics.[45] His contribution to the field was especially methodological in nature. He was already as early as in 1860 convinced that economics had essentially to be mathematical, which was furthermore one of the factors that led him to leave Australia, come back to England and study mathematics.[46]

Jevons was strongly influenced by Bentham’s utilitarianism and was devoted to mathematising it.[47] He identified an inherent mathematical character in Bentham’s work by quoting him from his ’Introduction to the Principles of Morals and Legislation’:

“Sum up all the values of all pleasures on the one side, and those of all the pains on the other. The balance, if it be on the side of pleasure, will give good tendency of the act upon the whole, with respect to the interests of that individual person; if on the side of pain, the bad tendency of it upon the whole.”[48]

However, quantifying human behaviour and feelings in a way to make the application of mathematical methods useful posed one of the most difficult problems to overcome. It basically meant making the model of the economic man thin enough to be applicable to mathematical methods.[49] If Jevons would have worked with a an economic man as complex and thick as the conception in Adam Smith’s work, it would have been impossible to mathematically reason with it.[50] Jevons reduced Bentham’s utility analysis from seven to the two circumstances, intensity and duration, which were of economic importance to him.[51] As a consequence of this reinterpretation of utility he made differential calculus applicable to economics, since both intensity and duration are quantifiable.[52] Furthermore, by reducing Bentham’s utility analysis Jevons explicitly separated economics from the realm of morals.[53] This reduction of economic man to simple mechanical acts of behaviour is advancing the overarching process of the reification of economics and the human subject. Jevons stated his intention to reify economics to a science guided by mechanical principles very openly:

“But as all the physical sciences have their basis more or less obviously in the general principles of mechanics, so all branches and divisions of economic science must be pervaded by certain general principles.”[54]

This reification of the human subject to a mechanical machine is even more clearly seen in Francis Edgeworth’s work who was himself a pioneer of mathematical and neoclassical economics and a close friend of Jevons. Closing the first part of his ’Mathematical Psychics’ Edgeworth writes:

“…at least the conception of Man as a pleasure machine may justify and facilitate the employment of mechanical terms and Mathematical reasoning in social science.”[55]

In this argumentation, we do not only see the eagerness to apply mathematical methods to economics but also to transfer concepts from the realm of physics. The term pleasure machine is in this sense by no means a coincidence and literally the embodiment of the reification of the human subject. A terminology that is similarly found in the 20th century, for example in Frank Knight’s work, where he refers to the economic man as a slot machine.[56]

Returning to Jevons work, there were two further important conceptualisations necessary to enable economics to measure and calculate utility. First, Jevons articulated the idea that not the utility itself needs to be measurable but only their effects on measurable magnitudes.[57] Second, he proposed the idea that one doesn’t need to measure the total utilities but only the marginal utility.[58] In that sense, Jevons found a way to combine utilitarianism, marginalism and mathematics.

It’s clear from Jevons’ work that he had no doubt about the usefulness of mathematics in economics and even saw it as a necessity to true economic theory. This made him one of the strongest advocates of mathematical economics and gave ground for Marshall’s criticism of excessive formalism.

Alfred Marshall – steering a middle ground

The influential English economist Alfred Marshall (1842-1924) is particularly interesting in regard of his attitude towards mathematical economics. Because his views on the usefulness of mathematics seem to be ambivalent, he was referred to both as being a proponent of mathematics but also as being an opponent of excessive use of mathematics in economics. His relationship to the use of mathematics seems to have been complex. It’s without question that Marshall expressed different opinions on mathematical economics over the course of his life.[59] Especially in his early days as a scholar, Marshall, a trained Cambridge mathematician, regarded mathematics as a very favourable tool to do economics.[60] As his career advanced, he seems to have become increasingly sceptical of mathematics, as can be seen in one of his most famous quotes, in which he famously noted to “burn the mathematics” in a letter he wrote to Arthur Bowley  in February 1906:

“I never read mathematics now: in fact I have forgotten even how to integrate a good many things. But I know I had a growing feeling in the later years of my work at the subject that a good mathematical theorem dealing with economic hypotheses was very unlikely to be good economics: and I went more and more on the rules — (1) Use mathematics as a shorthand language, rather than as an engine of inquiry. (2) Keep to them till you have done. (3) Translate into English. (4) Then illustrate by examples that are important in real life. (5) Burn the mathematics. (6) If you can't succeed in 4, burn 3. This last I did often...”[61]

This change in his view is particularly interesting, because it can be interpreted from two different perspectives. Numerus scholars see the change in this regard as a sign of Marshall himself changing, whereas mathematics would stay more or less unchanged.[62] Others argue that it was not so much Marshall who changed over the course of his life, but more the field of mathematics that changed and was becoming increasingly unfamiliar to a mathematician having gone through the traditional training at Cambridge.[63] As a result of this it’s often noted that in the beginning of his career his mathematical training was superior to that of most economists of his generation, but for example, Edgeworth and Pareto are considered more skilful in mathematics probably because Marshall didn’t care to keep up with the latest advancements in the field of mathematics.[64]

It seems likely that it was a combination of both of these developments. He was an admirer of mathematics but became throughout his career, because of his difficulties to empirically underline his theory, increasingly sceptical of pure mathematical approaches.[65] The importance that Marshall laid on empirical evidence also might indicate, why he was somewhat receptive to arguments from the German Historical School, as they strongly criticised a purely deductive approach and mathematical formalism.[66] In that sense, Marshall was not against mathematical elaborations as long as realism would not suffer.[67] He was both highly sceptical of excessive formalism but also of naïve empiricism.[68] For him, economic theory was an essential precondition for empirical investigation.[69] Therefore he saw great use in mathematics as a tool to construct and develop an economic theory as well as a tool for reasoning purposes, but he did not see in it the essence of the field of economics.[70]

This might be one reason why Marshall’s mathematical reasoning often lies beneath the surface.[71] He himself expressed the idea that mathematics should be kept in the background. [72] As a perfect illustration of this serves his use of diagrams. They serve as a very powerful thinking tool. In what Morgan calls “the experimental mode of graphs,” they allow conducting and following a line of reasoning that would be very difficult to perform verbally.[73] Marshall was obviously aware that graphs could also be represented in sets of equations but he preferred the graphical representation, because, among other things, they seem to be more accessible for the reader than algebra. [74] Although Marshall tried to keep the mathematics in the background, even his diagrams in his ‘Principles of Economics’ were kept in the footnotes, he made great use of mathematical reasoning.[75] 

Marshall had a very differentiated view on the use of mathematics in economics. He saw the benefits of these powerful tools in addressing economic problems but feared that its excessive use would detach the economists from the real facts of economic problems. This can be illustrated by Marshall’s comment on Edgeworth’s ‘Mathematical Psychics’ as Marshall wondered “how far he succeeds in preventing his mathematics from running away with him, and carrying him out of sight of the actual facts of economics.”[76] Echoing this, Arthur Pigou, one of Marshall’s pupils, commented Marshalls attitude towards mathematics as follows:

“Though a skilled mathematician, he used mathematics sparingly. He saw that excessive reliance on this instrument might lead us astray in pursuit of intellectual toys, imaginary problems not conforming to the conditions of real life: and further, might distort our sense of proportion by causing us to neglect factors that could not easily be worked up in the mathematical machine.”[77]

This fear that mathematics would drive economics away from realism led Marshall to become more sceptical of mathematical economics and to warn the field from its excessive use.[78]

Conclusion

The introduction of mathematics into economics in the 19th century was accompanied by a debate about the usefulness of mathematical economics that has continued – although increasingly in the background – until today. It is important to reiterate that it is in no way the purpose of this essay nor was it the purpose of many critics of mathematical economics to argue against the use of mathematics in economics in general. The intention of this essay is to provide the reader with some historical background on mathematical economics of the 19th century and to denaturalise its dominance of the field. It is with no doubt that the introduction of mathematics provided economics with powerful tools to conduct empirical studies and more abstract reasoning as well. It is, therefore, important to emphasis, quoting Sivlia Palasca, that “the debate over the usefulness of mathematics in economics should be regarded as a matter of degree and the appropriateness of the instrument for the intended use.”[79]

But considering this statement by Palasca, there appears to exist a striking difference between today’s economics and the field of the 19th century. Whereas in the 19th century economists applying mathematical methods felt the need to justify and legitimise their use of mathematics, today’s economists very rarely discuss the appropriateness of mathematics for their approaches. It seems that mathematics as become the standard tool of inquiry that is taken for granted by the entire field. The worries articulated by 19th century critics have stayed mostly unheard in the conquest of mathematics over the 20th century. So, although there was a strikingly high number of prominent mathematical economists in the 20th century, as being fine connoisseurs in mathematics made them fundamentally aware of its limits, echoing Marshall’s worry that excessive or false use of mathematics might carry the field away from reality, it didn’t limit the dominance of mathematics.[80] Partly because even though they occasionally expressed such worries they made widespread use of these mathematical tools.

As one of the only prominent economists who was not highly sophisticated in the artisanry of mathematics Joan Robinson was more fundamentally critiquing the excessive use of mathematics. She is famously quoted: “I never learned math so I had to think.”[81] Revolting against the marginalist tradition she used economics to address big structural economic and social questions. In 1976 Robert Aaron Gordon diagnosed his field with the incapability to address the big structural question of the world by relying solely on mathematical tools.[82] So although mathematics conquered economics in the 20th century there exists pluralist economics beyond this tradition until today.

In any case, students of economics are well advised to study the history of economics and remain sceptical of theories and methods presented to them. In the wake of the economic downturn caused by the corona pandemic, economics will need to provide solutions beyond screwing at the margins. The current (economic) crisis around the corona pandemic requires the capability to address structural questions. A diverse discussion and good judgement are needed to address the enormous challenges the world economy is facing. This means that the methodological repertoire of the economic profession is in urgent need of diversification. Taking the warnings of Marshall and others, who worried about the state of economics, seriously, provides a chance to potentially bring economics closer to reality and find answers to the big challenges that the world economy is facing.

Bibliography

Bhimani, Alnoor. „Accounting and the Emergence of “Economic Man”“. Accounting, Organizations and Society 19, Nr. 8 (November 1994): 637–74. https://doi.org/10.1016/0361-3682(94)90028-0.

Black, R. D. Collison. „Jevons, Bentham and De Morgan“. Economica 39, Nr. 154 (Mai 1972): 119. https://doi.org/10.2307/2552637.

Brodbeck, Karl-Heinz. Die Herrschaft des Geldes: Geschichte und Systematik. 2.Auflage. Darmstadt: Wissenschaftliche Buchgesellschaft, 2012.

Cairnes, John Elliott. The Character and Logical Method of Political Economy. Kitchener, Ont.: Batoche, 2001. http://site.ebrary.com/id/2001978.

Dardi, Marco. „Alfred Marshall and Mathematics“. In 9th European Society for the History of Economic Thought Conference–Stirling, Scotland, 2005.

Dupuit, Jules. „On the Measurement of the Utility of Public Works“. In Readings in Welfare Economics, herausgegeben von Kenneth J. Arrow und Tibor Scitovsky, 255–83. Homewood, IL: Richard D. Irwin, 1969.

Edgeworth, F. Y. Mathematical Psychics: An Essay on the Application of Mathematics to the Moral Sciences. London: C. Kegan Paul & Co., 1881.

Fisher, Irving. The Purchasing Power of Money - Its determination and relation to credit, interest and crises. New York: The Macmillan Company, 1922.

Gossen, H.H. The Laws of Human Relations and the Rules of Human Action Dereived Therefrom. Übersetzt von R.C. Blitz. Cambridge, Mass.: MIT Press, 1983.

Hill, Lisa. „Adam Smith on ’Thumos’ and Irrational Economic ‘Man’“. The European Journal of the History of Economic Thought 19, Nr. 1 (February 2012): 1–22. https://doi.org/10.1080/09672561003632550.

Hodgson, Geoffrey M. „Alfred Marshall versus the historical school?“ Journal of Economic Studies 32, Nr. 4 (2005): 331–348.

———. „Come Back Marshall, All Is Forgiven? Complexity, Evolution, Mathematics and Marshallian Exceptionalism“. The European Journal of the History of Economic Thought 20, Nr. 6 (December 2013): 957–81. https://doi.org/10.1080/09672567.2013.815245.

———. „On the Complexity of Economic Reality and the History of the use of Mathematics in Economics“. Filosofia de la Economia 1, Nr. 1 (2013): 25–43.

———. „The Evolution of Morality and the End of Economic Man“. Journal of Evolutionary Economics 24, Nr. 1 (January 2014): 83–106. https://doi.org/10.1007/s00191-013-0306-8.

Hudson, Michael. „The Use and Abuse of Mathematical Economics“. Real-World Economics Review, Nr. 55 (2010): 2–22. https://doi.org/10.1108/01443580010341754.

Jevons, William Stanley. The Theory of Political Economy. 3. Edition. London and New York: MacMillan and Co., 1888.

Keynes, John Maynard. Essays in Biography. Herausgegeben von Elizabeth Johnson und Donald Moggridge. 5. Edition. Bd. 10. The Collected Writings of John Maynard Keynes. Cambridge: Cambridge University Press, 2013. https://doi.org/10.1017/UPO9781139524230.

Lawson, Tony. „Really Reorienting Modern Economics“. Paper Presented at the INET Conference, April 2010, 1–21.

———. Reorienting Economics. London and New York: Routledge, 2003.

Maas, Harro. „Mechanical Rationality: Jevons and the Making of Economic Man“. Studies in History and Philosophy of Science Part A 30, Nr. 4 (December 1999): 587–619. https://doi.org/10.1016/S0039-3681(99)00030-8.

Malthus, Thomas. Principles of Political Economy: considered with a View to Their Practical Application. 2. Edition. London: Pickering, 1836.

Marshall, Alfred. Principles of Economics. Palgrave Classics in Economics. Basingstoke; New York: Palgrave Macmillan, 2013.

Mirowski, Philip. More Heat than Light: Economics as Social Physics, Physics as Nature’s Economics. Historical Perspectives on Modern Economics. Cambridge ; New York: Cambridge University Press, 1989.

Morgan, Mary S. „Economic Man as Model Man: Ideal Types, Idealization and Caricatures“. Journal of the History of Economic Thought 28, Nr. 1 (March 2006): 1–27. https://doi.org/10.1080/10427710500509763.

———. „Learning from models“. In Models as Mediators: Perspectives on Natural and Social Science, edited by Mary S. Morgan and Margaret Morrison, 347–88. Cambridge: Cambridge University Press, 1999.

———. The world in the model: how economists work and think. Cambridge ; New York: Cambridge University Press, 2012.

Morgenstern, Oskar. „Limits to the Uses of Mathematics in Economics“. Econometric Research Program. Research Memorandum. Princeton University, January 1963.

Myers, Milton. The Soul of the Modern Economic Man. Chicago and London: The University of Chicago Press, 1983.

Palasca, Silvia. „Mathematics in Economics. A Perspective on Necessity and Sufficiency“. Theoretical and Applied Economics 20, Nr. 9 (2013): 127–44.

Persky, Joseph. „Retrospectives: The Ethology of ’Homo Economicus’“. Journal of Economic Perspectives 9, Nr. 2 (Mai 1995): 221–31. https://doi.org/10.1257/jep.9.2.221.

Pheby, John. Methodology and Economics. London: Palgrave Macmillan UK, 1988. https://doi.org/10.1007/978-1-349-19258-8.

Pigou, A.C., Ed. Memorials of Alfred Marshall. London: Macmillan, 1925.

Quddus, Munir, und Salim Rashid. „Mathematics delayed? British economics: 1730-1870“. History of Economic Ideas, 2000, 39–75.

Reiss, Julian. „Mathematics in Economics: Schmoller, Menger and Jevons“. Journal of Economic Studies 27, Nr. 4/5 (August 2000): 477–91. https://doi.org/10.1108/01443580010342393.

Rubinstein, Ariel. „John Nash: The Master of Economic Modeling“. The Scandinavian Journal of Economics 97, Nr. 1 (March 1995): 9–13. https://doi.org/10.2307/3440824.

Schabas, Margaret. „Alfred Marshall, W. Stanley Jevons, and the mathematization of economics“. Isis 80, Nr. 1 (1989): 60–73.

Snowdon, Brian, und Howard R. Vane. Conversations with Leading Economists: Interpreting Modern Macroeconomics. Cheltenham, UK ; Northampton, MA, USA: Edward Elgar, 1999.

Stigler, G., F. Stigler, und C. Friedland. „The Journals of Economics“. Journal of Political Economy 105, Nr. 2 (1995): 331–59.

Theocharis, Reghinos D. Early Developments in Mathematical Economics. London: Palgrave Macmillan UK, 1983. https://doi.org/10.1007/978-1-349-04949-3.

———. The Development of Mathematical Economics. London: Palgrave Macmillan UK, 1993. https://doi.org/10.1007/978-1-349-12992-8.

Vazquez, Andres. „Marshall and the Mathematization of Economics“. Journal of the History of Economic Thought 17, Nr. 02 (September 1995): 247. https://doi.org/10.1017/S1053837200002625.

Weintraub, E. Roy. How Economics became a Mathematical Science. Durham and London: Duke University Press, 2002.

Wilson, David, und William Dixon. A History of Homo Economicus. Paperback Edition. Routledge Studies in the History of Economics. London and New York: Routledge, 2014.