The ergodicity problem in economics
Nature Physics
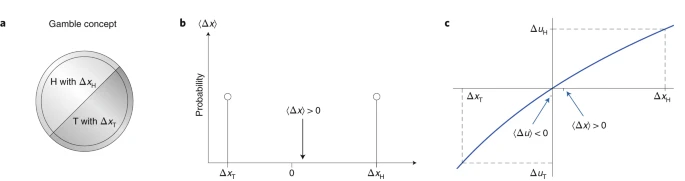
The ergodic hypothesis is a key analytical device of equilibrium statistical mechanics. It underlies the assumption that the time average and the expectation value of an observable are the same. Where it is valid, dynamical descriptions can often be replaced with much simpler probabilistic ones — time is essentially eliminated from the models. The conditions for validity are restrictive, even more so for non-equilibrium systems. Economics typically deals with systems far from equilibrium — specifically with models of growth. It may therefore come as a surprise to learn that the prevailing formulations of economic theory — expected utility theory and its descendants — make an indiscriminate assumption of ergodicity. This is largely because foundational concepts to do with risk and randomness originated in seventeenth-century economics, predating by some 200 years the concept of ergodicity, which arose in nineteenth-century physics. In this Perspective, the author argues that by carefully addressing the question of ergodicity, many puzzles besetting the current economic formalism are resolved in a natural and empirically testable way.
Comment from our editors:
The ergodicity economics programme has the potential to be one of the most groundbreaking challenges to economic orthodoxy to date. While much of behavioral economics is simply tinkering with utility functions or belief-formation, ergodicity economics changes the quantity to be maximized itself and looks now at the time average growth rate of stochastic processes. It takes accepted concepts, such as the noisy multiplicative growth processes underlying much of contemporary discussion about top wealth shares or the Kelly criterion as the cornerstone of intertemporal portfolio choice and puts them into a coherent framework to explicitly acknowledge this apparently neglected time dimension within contemporary decision theory. Unsurprisingly, it has also proven very controversial (cf. the replies to this article in Nature Physics), with many criticisms claiming that ergodicity economics either lacks novelty or is too simplistic. The jury is still out on the merits and empirical applicability, but any economist interested in the conceptual foundations of her discipline will most likely benefit from engaging with this perspective - if only to clarify the often unstated assumptions or domains of application of contemporary expected utility theory. For readers not too familiar with those concepts, Ole Peters' 2011 lecture at Gresham college is a very accessible introduction to the basic intuition and findings, which can be found here:
Time for a Change (YouTube video)
Go to: The ergodicity problem in economics