A Theory of Enormous Gravity

By Cahal Moran

Understanding international trade is central to economics and is currently a hot political issue. It’s an area where popular perceptions of mainstream economics are low, since they have historically missed some important downsides of trade agreements, especially the hollowing out of former manufacturing hubs in the Western world. Yet economists have for long time had a theory of trade with an impressive amount of scientific clout behind it: the gravity trade model. At its core this is a fairly simple model of trade which states that countries trade more if they are richer and/or closer together. While it cannot answer all our political questions about trade, it’s a good example of quantitative economics working well. Gravity trade models are a sharp riposte to those who do not believe mathematical models have scientific value in economics.

Stephen Hawking once commented that every equation in his famous book The Universe in a Nutshell would halve sales. At the risk of reducing the readership of this blog from 4 to 1, in this case I think it’s worth reproducing both the original gravity equation and its economic variant. According to Newton’s Laws, the amount of gravitational force F between two bodies (say, planets), Body 1 and Body 2, is given by:

Where m is the mass of a body and r is the distance between the centres of their masses, while G is a parameter known as the gravitational constant. In economics this can be modified to relate the trade between countries:

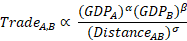
This looks a little more complicated, but all it means is that trade between two countries, Country A and Country B, increases with the Gross Domestic Product (GDP) of those countries and decreases with the physical distance between the two countries. Put plainly: the richer they are, the more they trade; the further away they are, the less they trade. The little parameters α, β, and σ just scale the equation, determining exactly how much of an effect the variables GDP and Distance have. Estimating this equation on real data introduces a few more complications, but the main message of the equation is preserved – and such a precise mapping from theory to empirics is unusual in economics.

Now, I know what you’re thinking. Economics has fairly been accused of riffing ideas from physics (without the associated scientific discipline), and now I’m showcasing an example where economists literally, transparently and unashamedly plucked an equation measuring the behaviour of gravitational bodies and just…used it to model trade. Walter Isard, who in 1954 first floated the idea for what became gravity trade models, was explicit about wanting to “adapt the potential concept in widespread use in the physical sciences” to the potential trade between nations. It was in 1962 that Jan Tinbergen – arguably the father of macroeconomic modelling - proposed an equation very similar to the above, though he was sneakier and did not make direct reference to physics. In any case, the analogy is clear and the name ‘gravity trade models’ has stuck.

Evidence and Foundations

Whatever we may think of the strategy of importing equations from physical science, the facts are undeniable: gravity trade models work! Statistically speaking, they explain a large proportion of trade between countries and estimates of the parameters are remarkably stable over time. Table 1 is reproduced from a 1985 paper by Jeffrey Bergstrand. If you go across the columns from left to right, you go forward a decade or so but the estimated parameters do not change much (I have circled the most relevant rows in red to make this easier to see):

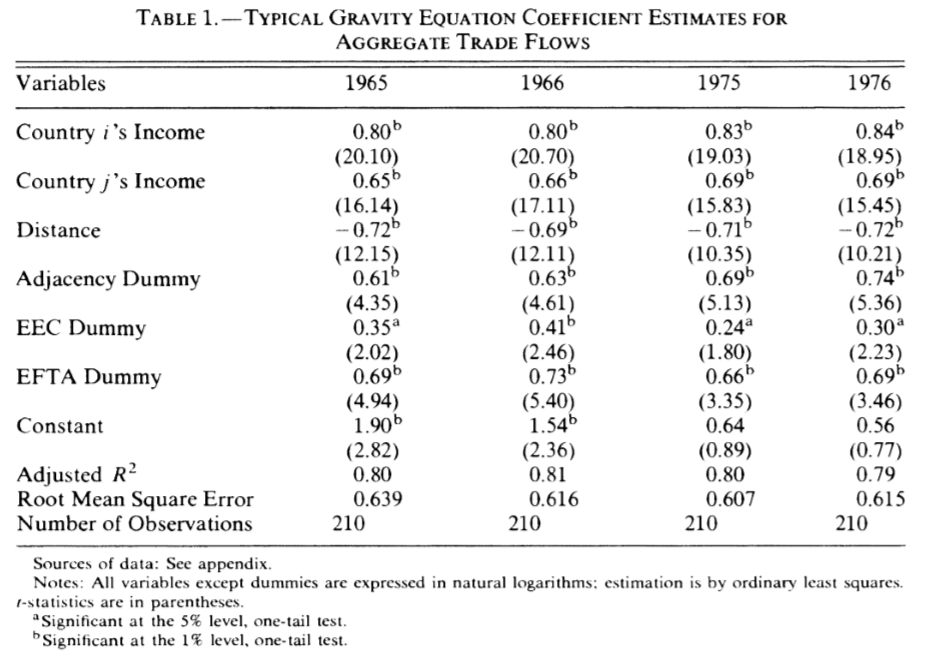
The fact that the parameters related to GDP and distance do not change much is a good sign we are estimating something that actually exists, as opposed to something which exists only within theory. Recall that in physics, the gravitational constant G is, well, constant – the equation wouldn’t be much use if it weren’t. In a well written 2014 review of the gravity trade model, Head and Mayer show in a meta-analysis of 1,835 estimates that the estimated parameters are both stable and close to one. Interpretation wise, this means that a 1% change in GDP of the importer, exporter, or in the distance between them, will result in a 1% change in trade.

The same review explores the theory behind the model in more depth. According to the authors early work on gravity trade models was characterised as above, thought of as having “dubious” empirical foundations and being the product of some “murky analogy with physics”. But it was shown over time that gravity-like relationships could emerge from standard economic models where distance played a role. What’s more, these models often implied some improvisation to the empirics: Bergstrand’s paper above built a model which implied that prices and exchange rates should be included in the analysis. Other innovations have resulted in estimations which take account of consumer preferences, different types of firms, and policy variables.

One of the curiosities of the literature was that during the 1990s, when commentators were confidently pronouncing the “death of distance” and “end of borders”, trade economists were using the gravity equation to show that distance consistently had an impact on trade. Many of the theories which aim to underpin gravity are quite elaborate but to my mind the most convincing attempt was by Thomas Chaney, who proposed an intuitive foundation for both the gravity model and the finding about distance. If large firms export over longer distances than small firms, but there are relatively few large firms, then these two effects cancel out and trade costs will be roughly constant even in the face of the kinds of big technological, demographic, and political changes to trade that we’ve seen over the past century or so. Chaney shows on French data that these assumptions about firms seem to be accurate.

Conclusions

One thing still missing from this literature - which would surely bolster any analogies with physics -are good predictions. To its credit, Tindenberg’s original paper actually tried to match predicted trade to real trade and admitted that “the relative deviations are quite considerable”. Since then it seems researchers have been happy with parameter stability, goodness of statistical fit, and improved theoretical underpinnings for the models. This is where politics comes back in: during the campaign for the United Kingdom to leave the European Union, gravity trade models were among those used to predict the fallout from leaving, but there is a lot of uncertainty in these estimates and so it will be hard to verify either way. All in all, it’s possible that the gravity trade model will remain our best way of understanding existing trade empirically, while acknowledging that new trade deals are probably too complicated for us to predict their consequences quantitatively.